Phương Trình Arrhenius: Công Thức Và Ý Nghĩa Trong Hóa Học

Trong hóa học động học, việc dự đoán tốc độ của một phản ứng hóa học là cực kỳ quan trọng. Phương trình Arrhenius chính là công cụ toán học nền tảng cho phép chúng ta thực hiện điều này, liên kết tốc độ phản ứng với nhiệt độ và năng lượng hoạt hóa (Ea) – rào cản năng lượng tối thiểu cần phải vượt qua để phản ứng xảy ra.

Bài viết này sẽ hướng dẫn chi tiết 3 phương pháp sử dụng phương trình Arrhenius, từ phân tích dữ liệu thực nghiệm đến dự đoán kết quả, giúp bạn làm chủ một trong những công thức cốt lõi nhất của hóa học.

Công thức phương trình Arrhenius:
k = A e^-Ea/(RT)

• k: Hằng số tốc độ phản ứng.
• A: Yếu tố tần số (liên quan đến tần suất va chạm hiệu quả giữa các phân tử).
• Ea: Năng lượng hoạt hóa (đơn vị: J/mol).
• R: Hằng số khí lý tưởng (8.314 J/mol·K).
• T: Nhiệt độ tuyệt đối (đơn vị: Kelvin).

Phương pháp 1: Xác định Năng Lượng Hoạt Hóa (Ea) từ Nhiều Nhiệt Độ

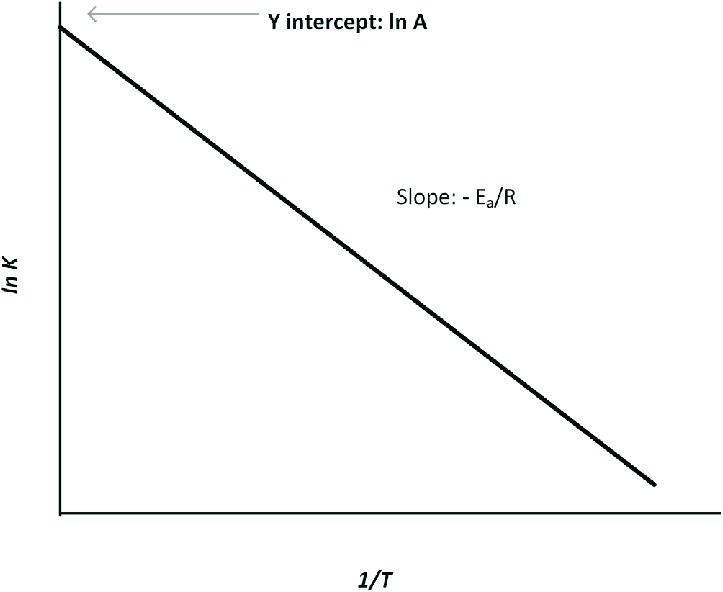
Đây là phương pháp chính xác nhất để xác định Ea bằng cách vẽ đồ thị logarit tự nhiên của hằng số tốc độ (ln k) theo nghịch đảo của nhiệt độ tuyệt đối (1/T). Độ dốc của đường thẳng thu được sẽ là -Ea/R.

Đây là phương pháp chuẩn mực, thường được sử dụng trong các nghiên cứu khoa học để xác định Ea một cách đáng tin cậy. Bằng cách thu thập dữ liệu hằng số tốc độ (k) ở nhiều mức nhiệt độ (T) khác nhau, chúng ta có thể vẽ đồ thị và tính toán chính xác.

Các bước thực hiện:

1. Chuẩn hóa đơn vị: Đảm bảo toàn bộ giá trị nhiệt độ được chuyển đổi sang Kelvin (K = °C + 273.15). Đây là bước bắt buộc để đảm bảo tính chính xác.
2. Biến đổi toán học: Lấy logarit tự nhiên (ln) của hằng số tốc độ (ln k) và tính nghịch đảo của nhiệt độ (1/T).
3. Vẽ đồ thị: Dựng đồ thị với trục tung (y) là ln k và trục hoành (x) là 1/T. Dữ liệu sẽ tạo thành một đường thẳng.
4. Tính toán: Độ dốc (slope) của đường thẳng này sẽ bằng -Ea/R. Từ đó, ta có thể suy ra năng lượng hoạt hóa: Ea = – (Độ dốc) × R

Ví dụ thực tế: Phản ứng chuyển hóa Cyclopropane thành Propene

Xét phản ứng đồng phân hóa từ Cyclopropane ⟶ Propene. Dữ liệu thực nghiệm cho thấy hằng số tốc độ k thay đổi theo nhiệt độ như sau: 0.00018 s⁻¹ (750 K), 0.0027 s⁻¹ (796 K), 0.030 s⁻¹ (850 K), 0.26 s⁻¹ (896 K).

Khi vẽ đồ thị ln k theo 1/T, ta thu được độ dốc là -3.27 × 10⁴ K.

⟶ Ea = -(-3.27 × 10⁴ K) × 8.314 J/mol·K ≈ 272,000 J/mol = 272 kJ/mol.

Đây chính là năng lượng cần thiết để phá vỡ liên kết trong vòng cyclopropane, cho phép nó sắp xếp lại thành propene.

 

Phương pháp 2: Ước tính Nhanh Ea từ Hai Điểm Dữ Liệu

Phương pháp này cho phép ước tính Ea nhanh chóng khi chỉ có hai cặp dữ liệu về nhiệt độ và hằng số tốc độ (T₁, k₁) và (T₂, k₂), sử dụng dạng phương trình so sánh.

Khi bạn không có đủ dữ liệu để vẽ đồ thị, phiên bản biến đổi của phương trình Arrhenius cho phép tính Ea chỉ từ hai cặp dữ liệu (T₁, k₁) và (T₂, k₂). Phương pháp này rất hữu ích để đưa ra ước tính nhanh chóng.

Công thức sử dụng:

ln(k₂/k₁) = (-Ea/R) * (1/T₂ – 1/T₁)

Các bước thực hiện:

1. Chọn hai cặp dữ liệu (T₁, k₁) và (T₂, k₂) và chuyển T sang Kelvin.
2. Tính tỷ số k₂/k₁ và sau đó lấy ln(k₂/k₁).
3. Tính hiệu số nghịch đảo nhiệt độ 1/T₁ - 1/T₂.
4. Áp dụng công thức trên để tìm Ea.

Lưu ý quan trọng: Phải nhất quán về thứ tự. Nếu bạn lấy ln(k₂/k₁) thì vế sau phải là 1/T₁ - 1/T₂. Một sự nhầm lẫn có thể dẫn đến kết quả Ea âm, một điều không thể xảy ra trong thực tế vì năng lượng hoạt hóa luôn là một rào cản dương.

Phương pháp 3: Dự Đoán Hằng Số Tốc Độ (k) tại Nhiệt Độ Mới

Khi đã biết Ea và một cặp dữ liệu (T₁, k₁), phương pháp này cho phép dự đoán chính xác hằng số tốc độ mới (k₂) tại một nhiệt độ mới (T₂), rất hữu ích cho ứng dụng công nghiệp.

Một ứng dụng mạnh mẽ của phương trình Arrhenius là dự đoán tốc độ phản ứng sẽ thay đổi như thế nào khi nhiệt độ thay đổi. Điều này cực kỳ giá trị trong kỹ thuật hóa học và thiết kế quy trình công nghiệp.

Công thức sử dụng (dạng tỷ lệ):

k₂ = k₁ * e^{(-Ea/R) * (1/T₂ – 1/T₁)}

Các bước thực hiện:

1. Bạn cần biết trước giá trị Ea của phản ứng.
2. Có một cặp dữ liệu đã biết (T₁, k₁).
3. Xác định nhiệt độ mới (T₂) mà bạn muốn dự đoán.
4. Thay tất cả các giá trị vào công thức để tính k₂.

Ví dụ: Một quy tắc kinh nghiệm phổ biến cho rằng tốc độ phản ứng thường tăng gấp đôi khi nhiệt độ tăng 10°C (hoặc 10 K). Điều này chỉ đúng với các phản ứng có Ea xấp xỉ 52 kJ/mol ở nhiệt độ phòng. Phương trình Arrhenius cung cấp một cách tính toán chính xác hơn nhiều so với quy tắc này.

So Sánh và Ứng Dụng Của 3 Phương Pháp

Phương Pháp	Ưu Điểm	Nhược Điểm	Ứng Dụng Chính
Từ nhiều nhiệt độ	Độ chính xác cao, giúp loại bỏ sai số	Yêu cầu nhiều dữ liệu thực nghiệm	Nghiên cứu động học, xác định cơ chế phản ứng.
Từ hai nhiệt độ	Nhanh chóng, đơn giản, không cần nhiều dữ liệu	Kém chính xác, nhạy cảm với sai số đo lường	Ước tính ban đầu, kiểm tra nhanh.
Dự đoán k	Có tính dự báo cao, hữu ích cho thiết kế	Độ chính xác phụ thuộc hoàn toàn vào Ea đã biết	Tối ưu hóa quy trình công nghiệp, an toàn phản ứng.

Những Lưu Ý Vàng Khi Áp Dụng Phương Trình Arrhenius

• Đơn vị là Vua: Luôn đảm bảo nhiệt độ tính bằng Kelvin (K). Sử dụng R = 8.314 J/mol·K và Ea tính bằng J/mol để thống nhất đơn vị.
• Chất Xúc Tác: Sự hiện diện của một chất xúc tác sẽ làm giảm năng lượng hoạt hóa Ea, dẫn đến việc tăng mạnh hằng số tốc độ k mà không cần thay đổi nhiệt độ. Phương trình Arrhenius mô tả hoàn hảo hiệu ứng này.
• Giới hạn của phương trình: Phương trình này giả định rằng Ea và A không đổi theo nhiệt độ, điều này thường đúng trong một khoảng nhiệt độ không quá lớn.

Câu Hỏi Thường Gặp (FAQs)

1. Yếu tố A trong công thức là gì?

A là yếu tố tần số, đại diện cho tần suất các va chạm xảy ra giữa các phân tử phản ứng theo đúng định hướng hình học để tạo ra sản phẩm.

Về mặt lý thuyết, A thể hiện số lần va chạm tối đa có thể xảy ra trong một đơn vị thời gian. Nó có thể được xác định bằng thực nghiệm từ giao điểm của đồ thị ln k vs 1/T với trục tung.

2. Tại sao Năng lượng hoạt hóa (Ea) không thể âm?

Ea không thể âm vì nó đại diện cho một rào cản năng lượng vật lý có thật mà các phân tử phải vượt qua. Giá trị âm là phi vật lý và thường là dấu hiệu của sai sót trong tính toán.

Một kết quả Ea âm sẽ ngụ ý rằng phản ứng sẽ xảy ra nhanh hơn ở nhiệt độ thấp hơn hoặc không cần năng lượng đầu vào, điều này mâu thuẫn với các nguyên tắc nhiệt động học và động học hóa học. Một kết quả Ea âm hầu như luôn do lỗi tính toán hoặc nhầm lẫn thứ tự trong công thức.

3. Chất xúc tác ảnh hưởng đến phương trình Arrhenius như thế nào?

Chất xúc tác làm tăng tốc độ phản ứng bằng cách cung cấp một con đường phản ứng thay thế có năng lượng hoạt hóa (Ea) thấp hơn, từ đó làm tăng mạnh giá trị hằng số tốc độ (k).

Theo phương trình Arrhenius, khi Ea giảm, giá trị của số mũ e-Ea/RT sẽ tăng lên đáng kể. Vì k tỷ lệ thuận với số mũ này, hằng số tốc độ k sẽ tăng vọt, làm cho phản ứng diễn ra nhanh hơn nhiều ở cùng một nhiệt độ.

Để tìm hiểu thêm về các khái niệm hóa học cơ bản và nâng cao, hoặc nếu bạn đang tìm kiếm một cửa hàng hóa chất uy tín, hãy truy cập website của Hóa Chất Doanh Tín để biết thêm chi tiết.